Table of Contents

• 数据结构
  • 数组
  • 链表
  • 队列
  • 栈
  • 散列表
    • Hash冲突
    • Ruby中的Hash实现原理
  • 图
    • 非加权图
    • 加权图
    • 负加权图
  • 树
    • 二叉树
    • B-树
    • B+树
    • 二叉堆
    • 红黑树

数据结构

数组

相同类型的变量的有序集合，在内存中顺序存储。相对比链表，适合读多写少的情况。

	读取	插入	删除
O(时间)	1	n	n

链表

在内存中随机存储，每个节点存储数据和下一个节点的指针。

	读取	插入	删除
O(时间)	n	1	1

队列

基于数组，先进先出 FIFO

比如，广度优先就是用这种数据结构去存储剩下需要访问的节点。

栈

基于数组，先进后出 FILO

比如，递归用的调用栈。递归太深了，一般都会抛错stack too deep。

散列表

通过Hash函数，将key转换为hashcode，然后再取模（模一般是散列表的长度），得到index，再在数组中查找index对应的数据。

	读取	插入	删除
O(时间)	1	1	1

Hash冲突

如果两个key对应的index是一样，这就是hash冲突。解决hash冲突有两种方式:

1. 开放寻址法 从对应的index开始，依次往后找空位，然后插入、读取。
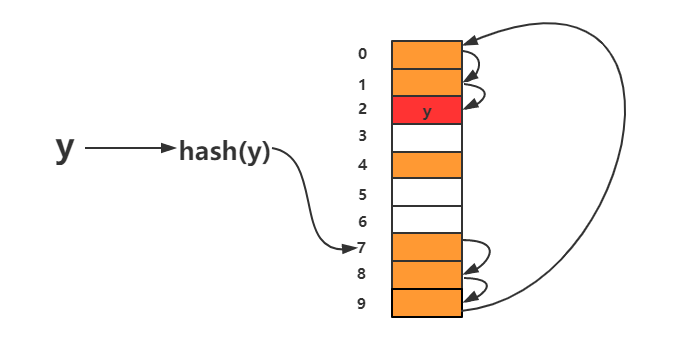
2. 链表法 即相同的key以链表的形式挂载在对应的index上。

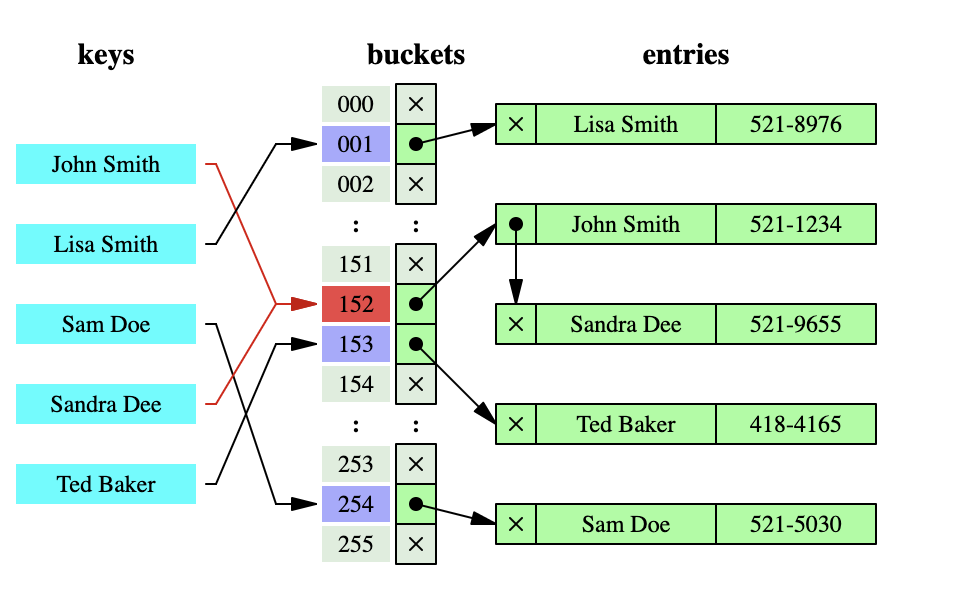
Ruby中的Hash实现原理

Ruby在2.4之前的Hash用的就是链表法。当链表的平均长度超过5的时候，就会扩容，并重新hash。在2.4引入了开放寻址法并进行了一些优化。4

图

非加权图

利用广度优先算法，可以得到：

1. 是否能够从起点到终点
2. 从起点到终点最近的线路

加权图

利用狄克斯特拉算法，可以得出从起点到终点最便宜的线路。需要注意环路的情况。

负加权图

利用贝尔曼-福特算法，可以得出从起点到终点最便宜的线路。需要注意环路的情况。

树

二叉树

每个父节点最多有两个子节点。

	读取	插入	删除
O(时间)	log n	log n	log n

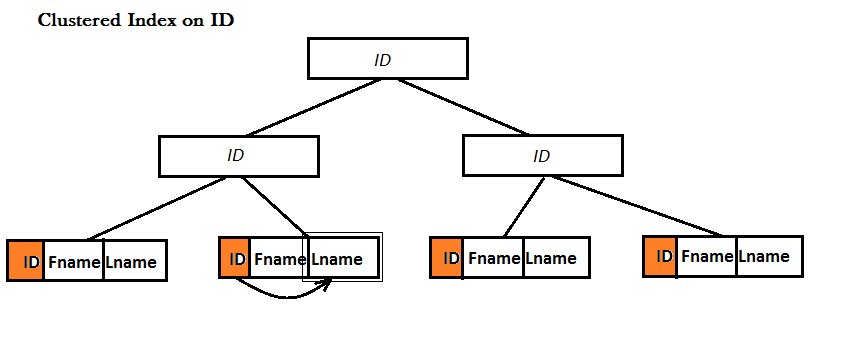
B-树

每一个节点包括多个孩子。这样的结果就是，每个节点包含更多的信息，相比二叉查找树，更加矮胖，这样可以减少磁盘的IO。1 相对比内存的操作，磁盘的IO才是瓶颈，所以要尽可能地把更多的index page放到内存里面操作。同时也引出一个index的设计原理，尽量index少的column。

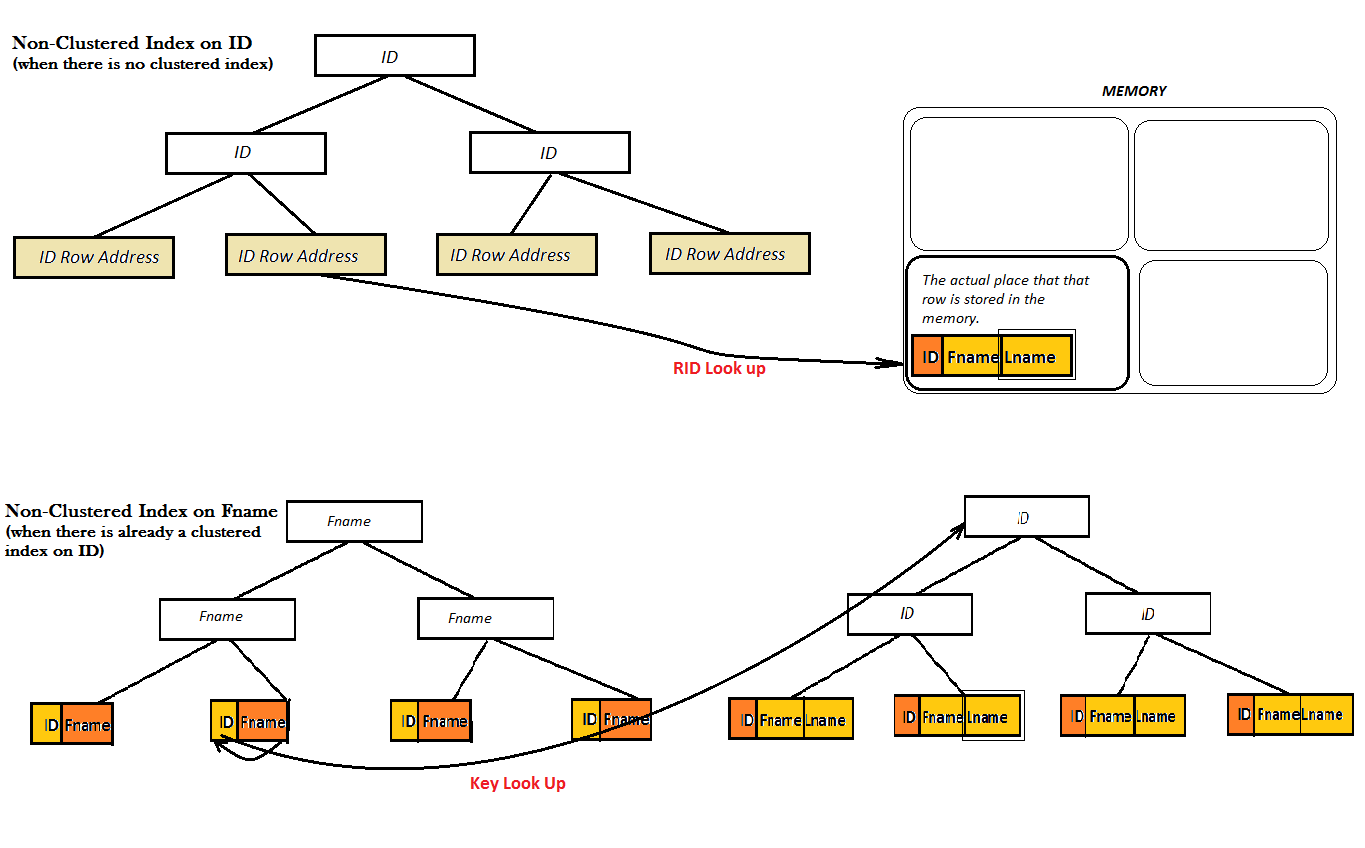
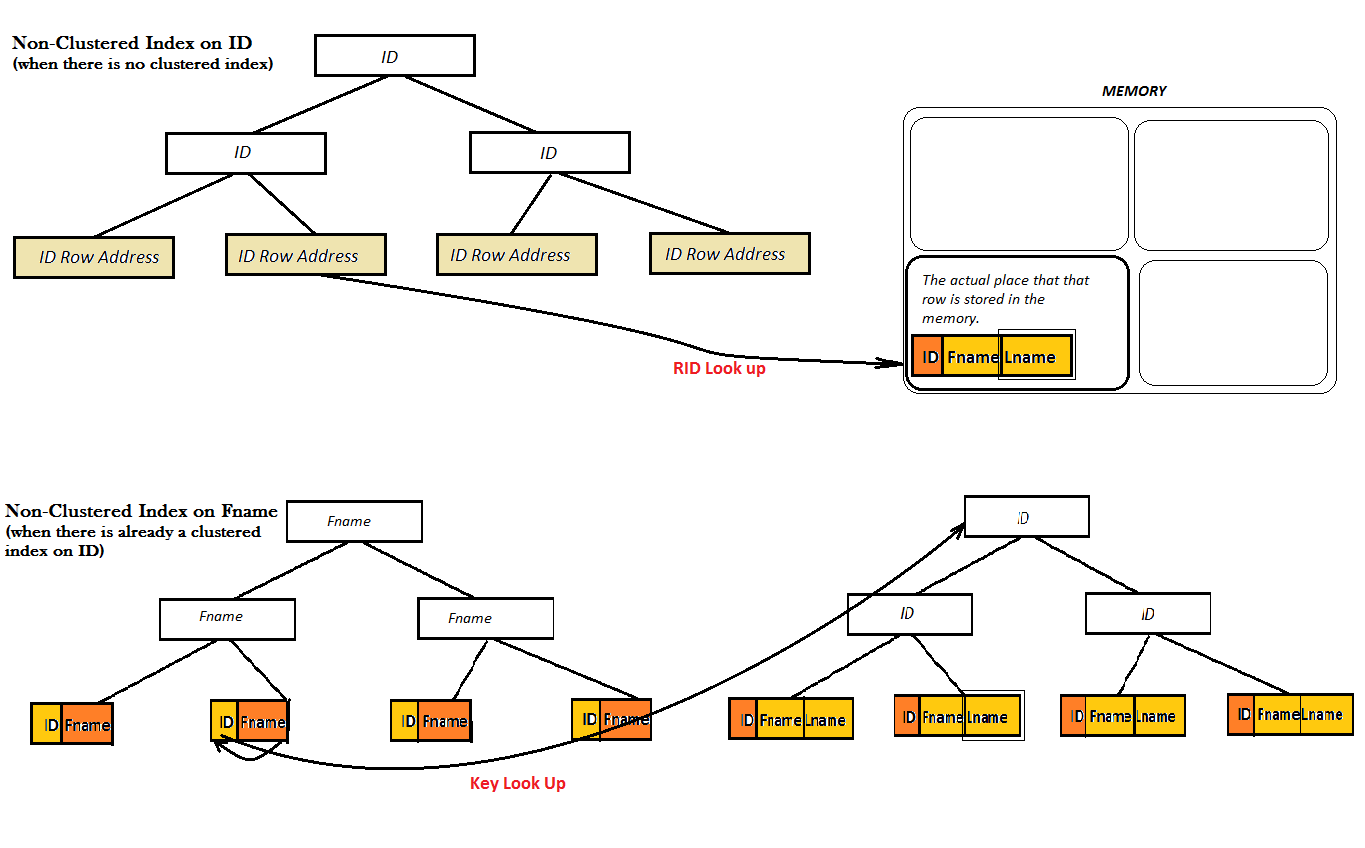
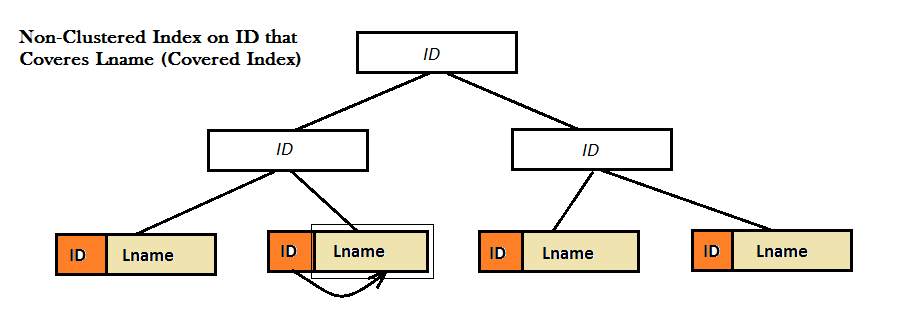
B+树

相对比B-树，中间节点只保存索引，不保存指针。叶节点保存中间节点的数据（即所有数据），记录的指针，以及所有叶节点的顺序链接。

SQL SERVER, MySQL的索引用的又是B+树。2

二叉堆

类似于二叉树，分为最大堆和最小堆

1. 最大堆 父节点比子节点大
2. 最小堆 父节点比子节点小

	读取	插入	删除
O(时间)	log n	log n	log n

红黑树

这个牵扯的太多了。先留坑吧。3